Classifying a Quadrilateral | Geometry How To Help

If you are reading this lesson, then you are pretty far through your geometry course. The focus of that course has probably concentrated on proving lines parallel and triangles congruent. In a traditional textbook, this is usually the first lesson in a unit about quadrilaterals. The two examples of this lesson model how to classify quadrilaterals with two methods: by all names that apply or the most precise name that applies. To be able classify quadrilaterals properly; you must know the definitions of quadrilateral and the special quadrilaterals.   

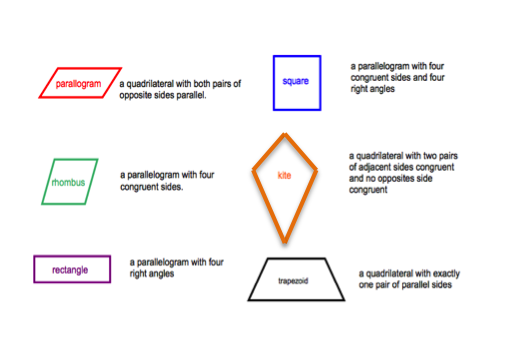
Definitions

Quadrilateral – four-sided figure

Parallelogram – a quadrilateral with both pairs of opposites sides parallel

Square – a parallelogram with four congruent sides and four right angles

Rhombus – a parallelogram with four congruent sides

Kite – a quadrilateral with two pairs of adjacent sides congruent and no opposite sides congruent

Rectangle – a parallelogram with four right angles

Trapezoid – a quadrilateral with exactly one pair of sides parallel

Isosceles Trapezoid – a trapezoid with the non-parallel sides congruent

Example 1 – Classifying a Quadrilateral

By appearance alone, classify the ABCD in as many ways as possible.

It is not usual for a person that is studying geometry to be asked to judge a shape by appearance alone, but in this case, that is what the directions ask you to do. If you are a verbal learner, then you are probably capable of just using the definitions to come up with your answer. A visual learner might find the above image with all the special quadrilaterals paired with their definitions. No matter how you learn best there are two names for ABCD:

1.     Quadrilateral

2.     Parallelogram

All too often, students tend to only name it a parallelogram because it has two pairs of opposite sides parallel. The directions to classify it in as many ways possible and by definition, it is also can be named a quadrilateral. It is very important to read and follow the directions to a problem carefully.

Example 2 – Connecting Algebra and Geometry

Determine the most precise name for the quadrilateral with vertices:

A(-2,1)

B(7,4)

C(4,-1)

D(-2,-3)

The connection between algebra and geometry in this example is the because the shape is given as vertices on the coordinate plane and to prove what this shape is relies on two skills: finding the slope of a line and finding the distance of a line segment. Finding the slope of a line is a skill taught in the typical Algebra 1 course and finding the length of a line segment is usually taught early on in a Geometry course.

To help the visual learner, I like to graph the points on graph paper and create the shape by connecting the vertices. I have done that in the above image. From the appearance of the shape it appears to be a trapezoid, because side AB appears to be parallel to side CD. Even though it appears to be a trapezoid, a proper coordinate proof finds the slope and distance of every side.

Slopes of Sides

After calculating the slopes, you can see that this is definitely a trapezoid because sides AB and CD have the same slope and the other sides do not, thus this quadrilateral has exactly one pair of parallel sides. Next, I have to prove the lengths of the sides. If sides BC and DA are the same length, then it would be an isosceles trapezoid, but based on the graph it does not appear those two sides are the same length.

Lengths of the Sides

Since no side is the same length, this is not an isosceles trapezoid and the most precise name for this quadrilateral is trapezoid.

Example 3 – Using Properties of Special Quadrilaterals

For the given kite, find the values of the variables and then find the lengths of the sides.

This example introduces how to use the geometry of special quadrilaterals to write an equation that needs to be solved.  Since the shape is a kite, by definition, there are two pairs of adjacent sides congruent. From the diagram, it is apparent that the top two sides are congruent and the bottom two sides are congruent. Since these sides are congruent we can write equations setting the algebraic expressions equal to each other:

2x – 12 = 2y – 10

3x – 2 = 2x + 7

To solve this system if equations, I will solve the blue equation first, because it has only one variable.

(1)     3x – 2 = 2x + 7    

(2)     x – 2 = 7    

(3)     x = 9

I change equation (1) into equation (2) by subtracting 2x from both sides. I change equation (2) into equation (3) by adding 2 to both sides and the value of x is 9. Now that I know the value of x, I substitute 9 into x in the orange equation.

(1)     2x – 12 = 2y – 10

(2)      2(9) – 12 = 2y – 10

(3)      18 – 12 = 2y – 10

(4)      6 = 2y – 10

(5)      16 = 2y

(6)      y = 8

To solve the orange equation, I first substitute 9 in for x, which gives equation (2). I simplify 2*9 to give equation (3), then simplify 18 – 12 to give equation (4). To get equation (5), I add 10 to both sides. Finally, I divide both sides by 2 and use the symmetric property of equality to turn the equation around to arrive at equation (6) and the second answer to this problem.

x = 9 and y = 8

To find the lengths of the sides, I substitute 9 for x and 8 for y into the algebraic expressions representing the lengths of the sides of the kite.

3x – 2 = 3(9) – 2 = 27 – 2 = 25

2x + 7 = 2(9) + 7 = 18 + 7 = 25

2x – 12 = 2(8) – 12 = 18 – 12 = 6

2y – 10 = 2(8) – 10 = 16 – 10 = 6

So, the lengths of the sides are 25, 25, 6, 6 and x = 9, while y = 8.

As you can see, solving geometry problems can rely heavily on Algebra skills.

Conclusion – Classifying Quadrilaterals

To be able to classify and solve problems with quadrilaterals, you need to the definitions of the special quadrilaterals. It is also important to keep your algebra skills sharp, because many times, solving problems with quadrilaterals requires solving equations or find the slope of lines.

Video Lesson on Classifying Quadrilaterals